7.3.3.2 Проверка соответствия теоретическому распределению с использованием критерия согласия хи-квадрат
В MS Excel критерий хи-квадрат реализован функцией ХИ2ТЕСТ . Эта функция вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Функция имеет параметры:
ХИ2ТЕСТ(фактический_интервал; ожидае-мый_интервал), где
- фактический_интервал – диапазон данных, который содержит результаты наблюдения, подлежащие сравнению с ожидаемыми значениями;
- ожидаемый_интервал – диапазон данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.
Для получения правильных результатов необходимо, чтобы объем выборки был не менее 40, выборочные данные сгруппированы в интервальный ряд с количеством интервалов не менее 7, а количество наблюдений в каждом интервале (частот) не менее 5.
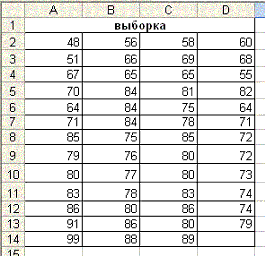
Пример 17. Проверить соответствие выборочных данных результатов сдачи экзаменов, оцененных в баллах: 48, 51, 67, 70, 64, 71, 85, 79, 80, 83, 86, 91, 99, 56, 66, 65, 84, 84, 84, 75, 76, 77, 78, 80, 86, 88, 58, 69, 65, 81, 75, 78, 85, 80, 80, 83, 86, 80, 89, 60, 68, 55, 82, 64, 71, 72, 72, 73, 74, 74, 79 нормальному закону распределения.
Решение
1. На рабочем листе подготовьте исходные данные в виде таблицы, содержащей баллы из приведенной выборки (См.рис.).

2. Выберите ширину интервала равную 5 баллам начиная от 50 до 95 и введите в диапазон F2:F11 граничные значения интервалов (см. рис.).

3. 3. Подготовьте заголовки создаваемой таблицы (ячейки G1, H1, I1)
4. Применяя функцию ЧАСТОТА заполните столбец абсолютных частот.
5. В ячейке H15 вычислите общее количество наблюдений, используя формулу =СУММ(G2:G11).
6.В ячейке Н16 вычислим среднее значение выборки, а в ячейке Н17 – стандартное отклонение.
7. Вычислите теоретические частости распределения. Поскольку мы проверяем соответствие заданной совокупности случайных величин нормальному закону распределения, то для расчета применим функцию НОРМРАСП. Установим курсор в ячейку H2 и вызовем из мастера функций функцию НОРМРАСП. Заполним поля аргу-ментов: x – F2, среднее – $Н$16, стандартное_откл. –$Н$17, ин-тегральный – 1, щелкнем на ОК.
8.В ячейку H3 введем формулу =НОРМРАСП(F3;$H$16;$H$17;1)-СУММ($H$2:H2) .
9. Скопируем введенную формулу в ячейки диапазона H4:H12.
10. Для вычисления теоретических частот установим курсор в ячейку I2 и введем формулу = $H$16* H2. Скопируем содержимое этой ячейки в ячейки диапазона I3:I12.
11.Используя функцию ХИ2ТЕСТ, определим соответствие данных выборки нормальному закону распределения. Для этого:
• установим курсор в свободную ячейку I15, включим Мастер функций, выберем категорию Статистические, а в списке функций – функцию ХИ2ТЕСТ;
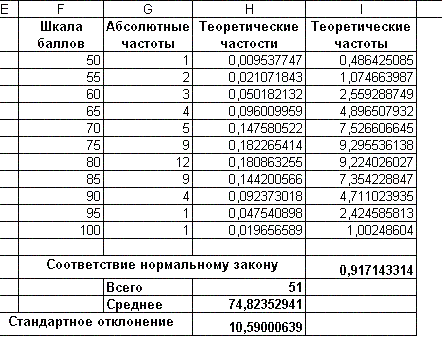
• заполним поля аргументов функции: фактический – введем адрес диа-пазона абсолютных частот G2:G12, ожидаемый – адрес диапазона тео-ретических частот I2: I12. После щелчка на кнопке ОК - в ячейке I15 будет вычислено значение вероятности того, что выборочные данные соответствуют нормальному закону распределения – 0,917143314. Поскольку полученная вероятность соответствия экспериментальных данных p = 0,917143314 намного больше уровня значимости α = 0,05, то можно утверждать, нулевая гипотеза не может быть отвергнута и эксперимен-тальные данные не противоречат нормальному закону распределения. Но, так как полученное значение вероятности очень мало отличается от 1, то можно говорить о высокой степени вероятности того, что эксперименталь-ные данные соответствуют нормальному закону.
Предыдущая Следующая Открыть содержание