7.2.3.2 Биноминальное распределение
Биноминальное распределение – одно из самых распространенных дискретных распределений, которое служит моделью для многих процессов. Для вычисления вероятности отдельного значения биноминального распреде-ления или значения случайной величины по заданной вероятности в табличном процессоре есть функции БИНОМРАСП и КРИТБИНОМ. Функция БИНОМРАСП применяется для вычисления вероятности в задачах с фиксированным числом испытаний или тестов, когда результатом любого испытания может быть только успех или неудача. Функция имеет параметры: БИНОМРАСП(число_успехов; число_испытаний; веорятность_успеха; интегральная), где
- число_успехов - количество успешных испытаний;
- число_испытаний – количество независимых испытаний;
- веорятность_успеха – вероятность успеха каждого испытания;
- интегральная – логическое значение, определяющее форму функции.
Если аргумент имеет значение ИСТИНА, то функция возвращает интегральную функцию распределения, т.е. вероятность того, что число успешных испытаний не менее значения аргумента число_успехов. Если этот аргумент имеет значение ЛОЖЬ, то вычисляется значение функции плотности распределения, т.е. вероятность того, что число успешных испытаний равно значению аргумента число_успехов.
Функция КРИТБИНОМ служит для вычисления наименьшего числа успешных исходов случайной величины, для которого интегральное биноминальное распределение больше или равно заданной величине (критерию). Функция имеет параметры: КРИТБИНОМ(число_испытаний; веорят-ность_успеха;альфа), где
- число_испытаний - количество независимых двухальтернативных испы-таний;
- веорятность_успеха - вероятность успеха каждого испытания;
- альфа – значение критерия, которое является уровнем значимости.
Пример 8. Банк выдает 5 кредитов. Вероятность невозврата кредита равна 0,2 для каждо-го из заемщиков. Требуется составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.
Решение
1. На рабочем листе подготовьте исходные данные для расчета:
- В ячейку А2 введите текст “Число испытаний”, а в ячейку В2 – количество выданных кредитов, число 5 (cм. рис.);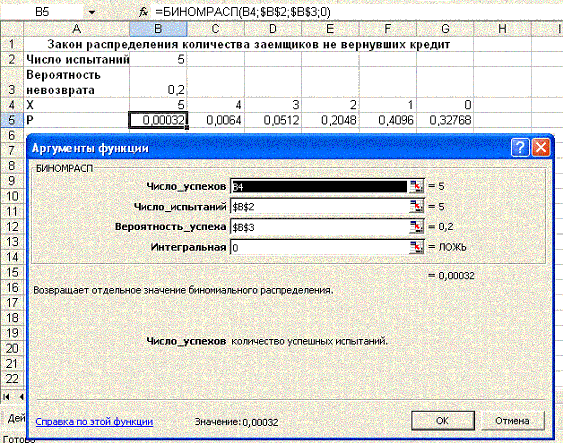
- В ячейку А3 введите текст “Вероятность невозврата”, а в ячейку В3 – значение вероятности невозврата кредита – число 0,2;
- в ячейку А4 введите текст “Х” – обозначающий случайную величину. В ячейку В4 введите число 5 – число заемщиков, не вернувших кредит. По-стройте последовательность членов арифметической прогрессии до ячейки G4 (см. рис. 8);
- В ячейку А5 введите текст “Р”, обозначающий вероятность невозврата кредита.
2. Установите курсор в ячейку В5. Выполните команду меню Вставка - Функция. В открывшемся окне диалога выберите категорию Статистические и функцию БИНОМРАСПР.
3. В соответствующих полях установите аргументы функции, делая ссылки на соответствующие ячейки, содержащие исходные данные (см. рис.). Аргументу Интегральная установите значение 0, что соответствует тому, что вероятность числа успешных испытаний будет равна значению аргумента Чис-ло_успехов.
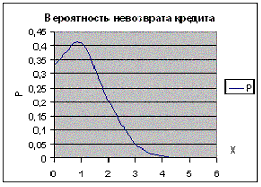
4. Установите для соответствующих аргументов абсолютные адреса, ис-пользуя клавишу F4. 5. Скопируйте полученную формулу в диапазон С4: G4. В ячейках диапазо-на В4 : C4 будет вычислен результат. 6. По данным полученной таблицы постройте график (cм. рис. ) Из таблицы и графика следует, что вероятность невозврата четырех и пяти кредитов очень мала, а вероятность невозврата одного кредита является самой большой и составляет величину 0,4096.

Пример 9. Для условий задачи предыдущего примера найти значение числа невозвращенных кредитов, для которого вероятность интегрального распределения больше или равна P>= 0,4.
Решение
1. Установите курсор в свободную ячейку рабочего листа. Выполните команду меню Вставка -Функция. В открывшемся окне диалога выберите категорию Статистические и функцию КРИТБИНОМ .
2. Введите значения параметров: число_испытаний – 5, веорятность_успеха – 0,2, альфа – 0,4 . После выполнения вычислений в ячейке будет получен результат равный 1.
Таким образом, при вероятности интегрального распределения P>= 0,4 будет не менее одного успешного события, т.е. не возвращенных кредитов будет не менее одного. Это также можно увидеть из графика.
Пример 10 . Построить диаграмму биноминальной функции плотности вероятности P(A=m) при n=10 и p=0,2.
Решение
1. Диапазон рабочего листа (А3: A13) заполните возможными значениями исходов испытаний: 0, 1, 2, …, 10 (cм. рис. ).
2. Установите курсор в ячейку В3 и выполните команду меню Вставка - Функция. В открывшемся окне диалога выберите категорию Статистические и в списке функций – БИНОМРАСП .
3. В диалоговом окне БИНОМРАСП заполните рабочие поля параметров:
- Число_успехов – введите количество успешных испытаний m, для чего щелкните на ячейке А3;
- Число_испытаний – введите общее количество проведенных испытаний – 10;
- Вероятность_успеха – введите величину вероятности успеха в каждом испытании 0,2;
- Интегральная – введите вид функции распределения (1) или весовая (0) – 0. После щелчка на кнопке ОК в ячейке В3 будет вычислена вероятность р=0,1073774 того, что из всех десяти испытаний будут все неудачные;
- Скопируйте формулу из ячейки В3 во все ячейки диапазона В4:B13.
- Полученную таблицу оформите так, как изображено на рисунке и постройте гистограмму плотности вероятности, как показано на рисунке.
Упражнение 5.
Книга издана тиражом 100 тыс. экземпляров. Вероятность брака в экземпляре равна 0,0001. Найти вероятность того, что тираж содержит 5 бракованных книг. (0,0378)
К предыдущей           К следующей    Открыть содержание