7 .2.3.3 Нормальный закон распределения
В табличном процессоре для вычисления значений нормального распределения есть специальные функции: НОРМРАСП, НОРМСТРАСП, НОРМОБР, НОРМСТОБР, и НОРМАЛИЗАЦИЯ. Функция НОРМРАСП вычисляет значения вероятности нормальной функции распределения для заданного среднего и стандартного отклонения. Она имеет параметры:
НОРМРАСП(x; среднее; стандартное_откл; интегральная), где
- x – значение, для которого строится распределение;
- среднее – среднее арифметическое распределения;
- стандартное_откл – стандартное отклонение распределения;
-интегральная – логическое значение, определяющее форму функции. Если этот параметр имеет значение ИСТИНА (1), то функция возвращает интегральную функцию распределения, в противном случае возвращает значение функции плотности распределения. Если среднее = 0 и стандартное_откл = 1, то функция вычисляет стандартное нормальное распределение. Для вычисления стандартного нормального распределения в библиотеке табличного процессора есть специальная функция НОРМСТРАСП. Она имеет параметры: НОРМСТРАСП(z), где z – значение случайной величины, для которого вычисляется распределение.
Функция НОРМОБР служит для вычисления квантилей для указанного среднего и стандартного отклонения (решается уравнение F(x) = p). Функция имеет параметры:
НОРМОБР(вероятность; среднее; стандартное_откл), где
- вероятность – вероятность, соответствующая нормальному распределению;
- среднее – среднее арифметическое распределения;
-стандартное_откл – стандартное отклонение распределения.
Функция НОРМСТОБР предназначена для вычисления квантилей стан-дартного нормального распределения, единственным ее параметром является вероятность. Функция НОРМАЛИЗАЦИЯ по заданному значению x и параметрам распределения вычисляет нормализованное значение, соответствующее x.
Пример 11. Постройте диаграмму нормальной функции плотности вероятности f(x) при М=24,3 и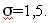
Решение
1. В ячейку А3 введите символ х, а в ячейку В3 – символ функции плотности вероятности f(x) (См.рис. ).
2. Вычислите нижнюю М-3сигма границу диапазона значений х, для чего установите курсор в ячейку С2 и введите формулу: =24,3-3*1,5, а также верхнюю границу – в ячейку Е2 введите формулу: =24,3+3*1,5.
3. Скопируйте формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифмети-ческой прогрессии.
4. Создайте последовательность значений х в требуемом диапазоне, для чего установите курсор в ячейку А4 и выполните команду меню Правка - Заполнить - Прогрессия.
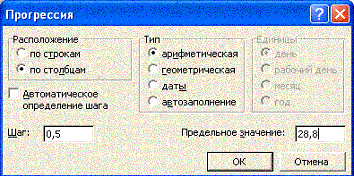
5. В открывшемся окне диалога Прогрессия (см. рис.) установите переключатели арифметическая, по столбцам, в поле Шаг введите значение 0,5, а в поле Предельное значение – число, равное верхней границе диапазона.

6. Щелкните на кнопке ОК. В диапазоне А4:А22 будет сформирована по-следовательность значений х.
7. Установите курсор в ячейку В4 и выполните команду меню Вставка - Функция. В открывшемся окне Мастер функций выберите категорию Статистические и в списке функций – НОРМРАСП.
8. Установите значения параметров функции НОРМРАСП: для параметра х установите ссылку на ячейку А4, для параметра Среднее – введите число 24,3, для параметра Стандартное_отклон число 1,5, для параметра Интегральное – число 0 (весовая). Рис. 11
9. Используя маркер буксировки, скопируйте полученную формулу в диапазон ячеек В5:D22. 10. Выделите диапазон полученных табличных значений функции f(x) (В3:B22) и выполните команду меню Вставка - Диаграмма. В окне Мас-тер диаграмм во вкладке Стандартные выберите График, а в окне Вид – вид графика, щелкните на кнопке Далее. 11. В окне Мастер диаграмм (шаг 2) выберите закладку Ряд. В поле Подписи оси х укажите ссылку на диапазон, содержащий значения х (А3:А22). Щелкните на кнопке Далее. 12. В окне Мастер диаграмм (шаг 3) введите подписи: Название диаграм-мы, Ось х, Ось y. Щелкните на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности.
Упражнение 6.
1. Постройте диаграмму стандартного нормального интегрального распре-деления. (стандартное нормальное распределение имеет M=0 и ?=1). Используйте функцию НОРМСТРАСП.
2. Вычислите верхнюю и нижнюю квартили для нормальной функции плотности вероятности f(x) при М=24,3 и сигма=1,5.
3. Вычислите вероятность того, что появится случайная величина х<= 42 при нормальном законе распределения вероятностей с М = 40 и Сигма = 1,5.
4. Вычислите квантиль для р=0,908789 и нормального распределения с М=20, сигма=1,5 и х=21.
5. Магазин продает мужские костюмы. Распределение спроса по размерам является нормальным с математическим ожиданием М=48 и сигма=2. Вычислите процент спроса на 50 размер. (17,6).
К предыдущему               К следующему    Открыть содержание