7.3.6 Использование инструментов табличного процессора для регрессионного анализа
Важную роль при исследовании взаимосвязей между статистическими выбор-ками кроме корреляционного и дисперсионного анализа играет регрессионный анализ. Регрессия позволяет проанализировать воздействие на какую-либо за-висимую переменную одной или более независимых переменных и позволяет установить аналитическую форму (модель) этой зависимости. Если рассматривается зависимость между одной зависимой переменной Y и не-сколькими независимыми X₁, X₂, …, X_n, то речь идет о множественной линей-ной регрессии. В этом случае уравнение регрессии имеет вид: Y = a₀ + a₁X₁ + a₂X₂ +…+a_nX_n, где a₁, a₂, …, a_n - коэффициенты при независимых переменных, которые нужно вычислить (коэффициенты регрессии), a₀ –константа. При построении регрессионной модели важнейшими моментами являются оценка ее адекватности (эффективности) и значимости, на основании которых можно судить о возможности применения в практике полученной модели. Мерой оценки адекватности регрессионной модели является коэффициент детерминации R2 (R-квадрат), который определяет, с какой степенью точности полученное уравнение регрессии аппроксимирует исходные данные. Значимость регрессионной модели оценивается с помощью критерия Фишера (F – критерия). Если величина F – критерия значима (р < 0,05), то регрессион-ная модель является значимой.
В MS Excel можно аппроксимировать экспериментальные данные линейным уравнением до 16 порядка: Y = a₀ + a₁X₁ + a₂X₂ +…+a₁₆X₁₆. Для вычисления ко-эффициентов регрессии служит инструмент Регрессия, который можно включить следующей последовательностью операций:
1. Выполнить команду Сервис - Анализ данных .
2. В раскрывшемся окне диалога Анализ данных выбрать из списка строку Регрессия – раскроется окно диалога Регрессия .
3. В группе Входные данные в поле Входной интервал Y указать адресную ссылку на диапазон, содержащий значения зависимой переменной, а в поле Входной интервал Х – ссылку на диапазон, содержащий значения независимых переменных, т.е. переменных влияние которых на зависимую переменную Y оценивается, установить флажок Метки, если исходная таблица имеет названия столбцов и флажок Константа-ноль , если а0=0.
4. В группе Параметры выхода указать, куда следует выводить результаты вычислений.
5. Если необходимо получить визуальную картинку отличия экспериментальных точек от предсказанных регрессионной моделью, то установить флажок График подбора .
6. Если нужно получить график нормальной вероятности, то установить флажок График нормальной вероятности .
В выходном диапазоне после выполнения вычислений отображаются результаты дисперсионного анализа, коэффициенты регрессии, стандартная погреш-ность вычисления Y, среднеквадратичные отклонения, количество наблюдений, стандартные погрешности для коэффициентов. Значения коэффициентов регрессии размещаются в столбце Коэффициенты:
- Y- пересечение a₀;
- X₁ - a₁; 
- X₁ – a₂ и т.д.
В столбце Р – Значение содержится оценка достоверности отличия соответствующих коэффициентов от нуля. Если P > 0,05, то коэффициент можно считать нулевым. Это означает, что соответствующая независимая переменная практически не влияет на зависимую переменную. Значение R – квадрат определяет, с какой степенью точности регресси-онное уравнение будет аппроксимировать экспериментальные данные. Если R – квадрат > 0,95, то точность аппроксимации высокая. При 0,8< R – квадрат< 0,95 аппроксимация удовлетворительная. В случае, когда R – квадрат <0,6, точность аппроксимации недостаточна и модель требует улучшения.
Кроме инструмента Регрессия в MS Excel для получения параметров уравнения регрессии есть функция ЛИНЕЙН и функция ТЕНДЕНЦИЯ для получения значения Y в требуемых точках.
Пример 20. Имеются статистические данные о затратах, связанных с рекламой по телевидению, с рекламой в метро и объеме реализации продукции в рублях, приведенные в таблице.

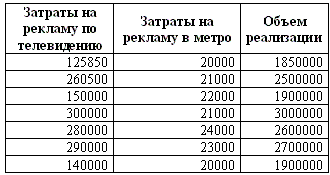
Требуется найти регрессионные коэффициенты для независимых переменных Затраты на рекламу по телевидению и Затраты на рекламу в метро на объем реализации продукции и построить уравнение регрессии.
Решение.
1. На рабочем листе в диапазон А1: С8 введите данные приведенной таблицы (см. рис.).
2. Включите инструмент Регрессия. В открывшемся диалоговом окне установите параметры (см. рис. ):

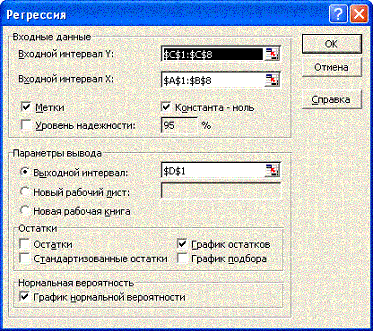
- Входной интервал Y – диапазон С1:C8;
- Входной интервал X – диапазон A1:B8;
- Переключатели Метки, Константа - ноль ;
-Выходной интервал – адрес D1;
- Флажок График нормальной вероятности;
- Флажок График остатков.
После щелчка на кнопке ОК в диапазон D1:L21 будет выведен результат регрессионного анализа.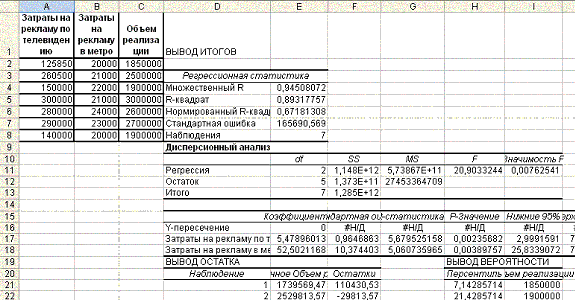
Полученные результаты:
1. Коэффициент детерминации R – квадрат = 0,893 ( аппроксимация удовле-творительная).
2. Значимость F = 0,00762 (р < 0,05- регрессионная модель значима).
3. Y – пересечение a₀ =0.
4. a₁= 5,478 – коэффициент при независимой переменной Затраты на рекламу по телевидению< /em> .
5. a₂ = 52,502 - коэффициент при независимой переменной Затраты на рекламу в метро.
С учетом полученных данных уравнение регрессии будет иметь вид:
Y= 5,478X₁ + 52,502X₂ , где
Х₁ – величина затрат на рекламу по телевидению ,
Х₂ – величина затрат на рекламу в метро.
       К предыдущей
Открыть содержание